“Yeah It’s on. ”
记录一下学习算法过程中沉淀下来的东西
正文
递归
https://www.cnblogs.com/huan-guo/p/8489905.html
关于递归的概念,我们都不陌生。简单的来说递归就是一个函数直接或间接地调用自身,是为直接或间接递归。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。用递归需要注意以下两点:
- 递归就是在过程或函数里调用自身。
- 在使用递归策略时,必须有一个明确的递归结束条件,称为递归出口。
递归一般用于解决三类问题:
- 数据的定义是按递归定义的。(Fibonacci函数,n的阶乘)
- 问题解法按递归实现。(回溯)
- 数据的结构形式是按递归定义的。(二叉树的遍历,图的搜索)
递归的缺点:
递归解题相对常用的算法如普通循环等,运行效率较低。因此,应该尽量避免使用递归,除非没有更好的算法或者某种特定情况,递归更为适合的时候。在递归调用的过程当中系统为每一层的返回点、局部量等开辟了栈来存储,因此递归次数过多容易造成栈溢出。
尾递归
https://www.cnblogs.com/huan-guo/p/8489905.html
http://www.ruanyifeng.com/blog/2015/04/tail-call.html
函数调用自身,称为递归。如果尾调用自身,就称为尾递归。
递归非常耗费内存,因为需要同时保存成千上百个调用记录,很容易发生”栈溢出”错误(stack overflow)。但对于尾递归来说,由于只存在一个调用记录,所以永远不会发生”栈溢出”错误。
顾名思义,尾递归就是从最后开始计算, 每递归一次就算出相应的结果, 也就是说, 函数调用出现在调用者函数的尾部, 因为是尾部, 所以根本没有必要去保存任何局部变量. 直接让被调用的函数返回时越过调用者, 返回到调用者的调用者去。尾递归就是把当前的运算结果(或路径)放在参数里传给下层函数,深层函数所面对的不是越来越简单的问题,而是越来越复杂的问题,因为参数里带有前面若干步的运算路径。
int FibonacciRecursive(int n)
{
if( n < 2)
return n;
return (FibonacciRecursive(n-1)+FibonacciRecursive(n-2));
}
尾递归是极其重要的,不用尾递归,函数的堆栈耗用难以估量,需要保存很多中间函数的堆栈。比如f(n, sum) = f(n-1) + value(n) + sum; 会保存n个函数调用堆栈,而使用尾递归f(n, sum) = f(n-1, sum+value(n)); 这样则只保留后一个函数堆栈即可,之前的可优化删去。
采用尾递归实现Fibonacci函数,程序如下所示:
int FibonacciTailRecursive(int n,int ret1,int ret2)
{
if(n==0)
return ret1;
return FibonacciTailRecursive(n-1,ret2,ret1+ret2);
}
递归函数的改写
尾递归的实现,往往需要改写递归函数,确保最后一步只调用自身。做到这一点的方法,就是把所有用到的内部变量改写成函数的参数。
尾调用优化
http://www.ruanyifeng.com/blog/2015/04/tail-call.html
尾调用之所以与其他调用不同,就在于它的特殊的调用位置。
我们知道,函数调用会在内存形成一个”调用记录”,又称”调用帧”(call frame),保存调用位置和内部变量等信息。如果在函数A的内部调用函数B,那么在A的调用记录上方,还会形成一个B的调用记录。等到B运行结束,将结果返回到A,B的调用记录才会消失。如果函数B内部还调用函数C,那就还有一个C的调用记录栈,以此类推。所有的调用记录,就形成一个“调用栈”(call stack)。
尾调用由于是函数的最后一步操作,所以不需要保留外层函数的调用记录,因为调用位置、内部变量等信息都不会再用到了,只要直接用内层函数的调用记录,取代外层函数的调用记录就可以了。
function f() {
let m = 1;
let n = 2;
return g(m + n);
}
f();
// 等同于
function f() {
return g(3);
}
f();
// 等同于
g(3);
上面代码中,如果函数g不是尾调用,函数f就需要保存内部变量m和n的值、g的调用位置等信息。但由于调用g之后,函数f就结束了,所以执行到最后一步,完全可以删除 f() 的调用记录,只保留 g(3) 的调用记录。
这就叫做”尾调用优化”(Tail call optimization),即只保留内层函数的调用记录。如果所有函数都是尾调用,那么完全可以做到每次执行时,调用记录只有一项,这将大大节省内存。这就是”尾调用优化”的意义。
数组
乱序一个数组
https://juejin.im/post/5d004ad95188257c6b518056
sort 结合 Math.random
这种方案其实是一种伪随机算法
/**
* 数组乱序
*/
function shuffle(arr) {
return arr.sort(() => Math.random() - 0.5);
}
这似乎是一个合理的解决方案。事实上在使用搜索引擎搜索“随机打乱数组”,这种方式会是出现最多的答案。
然而,这种方式并不是真正意思上的乱序,一些元素并没有机会相互比较, 最终数组元素停留位置的概率并不是完全随机的。
如果排序真的是随机的,那么每个元素在每个位置出现的概率都应该一样, 实验结果各个位置的数字应该很接近,而不是像现在这样各个位置的数字相差很大。
为什么会有问题呢?这需要从array.sort方法排序底层说起。
v8在处理sort方法时,使用了插入排序和快排两种方案。 当目标数组长度小于10时,使用插入排序;反之,使用快速排序。
其实不管用什么排序方法,大多数排序算法的时间复杂度介于O(n)到O(n²)之间, 元素之间的比较次数通常情况下要远小于n(n-1)/2, 也就意味着有一些元素之间根本就没机会相比较(也就没有了随机交换的可能), 这些 sort 随机排序的算法自然也不能真正随机。
其实我们想使用array.sort进行乱序,理想的方案或者说纯乱序的方案是数组中每两个元素都要进行比较, 这个比较有50%的交换位置概率。这样一来,总共比较次数一定为n(n-1)。 而在sort排序算法中,大多数情况都不会满足这样的条件。因而当然不是完全随机的结果了。
高性能的乱序算法 Fisher–Yates
为什么叫 Fisher–Yates 呢? 因为这个算法是由 Ronald Fisher 和 Frank Yates 首次提出的。
这个算法其实非常的简单,就是将数组从后向前遍历,然后将当前元素与它之前的随机位置的元素进行交换。
// 打乱数组
function shuffle(arr) {
let m = arr.length;
while (m > 1) {
let index = Math.floor(Math.random() * m--);
swap(arr, m, index);
}
return arr;
}
function swap(arr, i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
Fisher–Yates 算法只需要通过一次遍历即可将数组随机打乱顺序,性能极为优异~~
至此,我们找到了将数组乱序操作的最优办法
此外还有一个需要注意的细节,当前元素是可以和它本身互相交换的 - 否则生成最后的排列组合的概率就不对了 (对应上面就是m可能会和index相等 因为执行了 m– 再swap 所以是正确的)
数组排序
快速排序
var quickSort = function(arr) {
if (arr.length <= 1) { return arr; }
var pivotIndex = Math.floor(arr.length / 2); //基准位置(理论上可任意选取)
var pivot = arr.splice(pivotIndex, 1)[0]; //基准数
var left = [];
var right = [];
for (var i = 0; i < arr.length; i++){
if (arr[i] < pivot) {
left.push(arr[i]);
} else {
right.push(arr[i]);
}
}
return quickSort(left).concat([pivot], quickSort(right)); //链接左数组、基准数构成的数组、右数组
};
使用arr.splice是为了取出元素(返回删除值) concat只能链接数组
希尔排序
function selectionSort(arr) {
var len = arr.length;
var minIndex, temp;
for (var i = 0; i < len - 1; i++) {
minIndex = i;
for (var j = i + 1; j < len; j++) {
if (arr[j] < arr[minIndex]) { // 寻找最小的数
minIndex = j; // 将最小数的索引保存
}
}
temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
return arr;
}
堆排序
https://segmentfault.com/a/1190000015487916?utm_source=tag-newest
https://segmentfault.com/a/1190000015487916?utm_source=tag-newest
https://www.cnblogs.com/chengxiao/p/6129630.html
对于结点 i ,其子结点为 2i+1 与 2i+2 。
- 堆是一个完全二叉树。
- 完全二叉树: 二叉树除开最后一层,其他层结点数都达到最大,最后一层的所有结点都集中在左边(左边结点排列满的情况下,右边才能缺失结点)。
- 大顶堆:根结点为最大值,每个结点的值大于或等于其孩子结点的值。
- 小顶堆:根结点为最小值,每个结点的值小于或等于其孩子结点的值。
- 堆的存储: 堆由数组来实现,相当于对二叉树做层序遍历。
我们用简单的公式来描述一下堆的定义就是:
大顶堆:arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]
小顶堆:arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]
再简单总结下堆排序的基本思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素”沉”到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序。
代码实现:
function swap(A, i, j) {
let temp = A[i]
A[i] = A[j]
A[j] = temp
}
// 将 i 结点以下的堆整理为大顶堆,注意这一步实现的基础实际上是:
// 假设 结点 i 以下的子堆已经是一个大顶堆,shiftDown函数实现的
// 功能是实际上是:找到 结点 i 在包括结点 i 的堆中的正确位置。后面
// 将写一个 for 循环,从第一个非叶子结点开始,对每一个非叶子结点
// 都执行 shiftDown操作,所以就满足了结点 i 以下的子堆已经是一大
// 顶堆
function shiftDown(A, i, length) {
let temp = A[i]
// j<length 的目的是对结点 i 以下的结点全部做顺序调整
for (let j = 2 * i + 1; j < length; j = 2 * j + 1) {
temp = A[i] // 将 A[i] 取出,整个过程相当于找到 A[i] 应处于的位置
if (j + 1 < length && A[j] < A[j + 1]) {
j++ // 找到两个孩子中较大的一个,再与父节点比较
}
if (temp < A[j]) {
swap(A, i, j) // 如果父节点小于子节点:交换;否则跳出
i = j // 交换后,temp 的下标变为 j
} else {
break
}
}
}
function heapSort(A) {
// 初始化大顶堆,从第一个非叶子节点开始
for (let i = Math.floor(A.length / 2 - 1); i >= 0; i--) {
shiftDown(A, i, A.length)
}
for (let i = Math.floor(A.length - 1); i > 0; i--) {
// 根节点与最后一个节点交换
swap(A, 0, i)
// 从根节点开始调整,并且最后一个结点已经为当
// 前最大值,不需要再参与比较,所以第三个参数
// 为 i,即比较到最后一个结点前一个即可
shiftDown(A, 0, i)
}
return A
}
测试:
let arr = [4, 6, 8, 5, 9, 1, 2, 5, 3, 2]
const res = heapSort(arr)
console.log("res",res)
function push {
* 在堆尾部添加元素
* 执行上浮循环
* 与父元素对比大小,将较大的放在父节点位置
return minItem
}
桶排序
https://wiki.jikexueyuan.com/project/easy-learn-algorithm/bucket-sort.html
https://dailc.github.io/2016/12/03/baseKnowlenge_algorithm_sort_bucketSort.html
- 设置固定空桶数
- 将数据放到对应的空桶中
- 将每个不为空的桶进行排序
- 拼接不为空的桶中的数据,得到结果
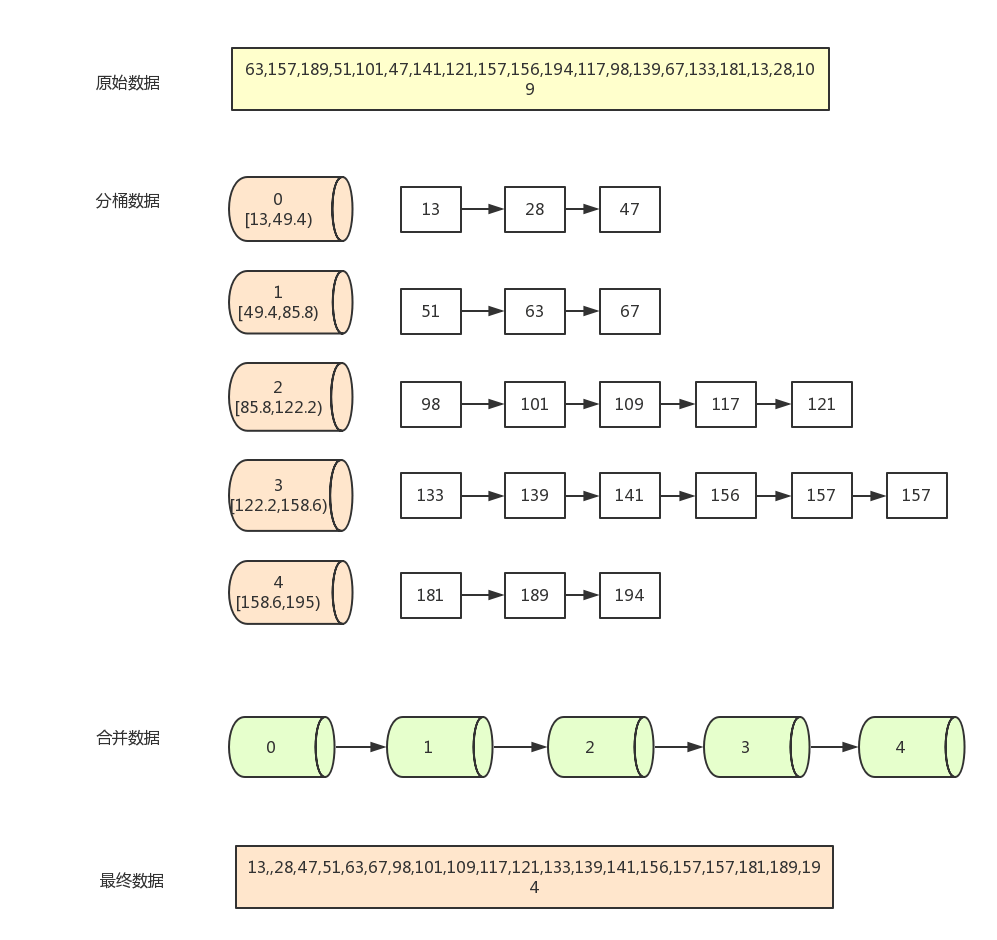
举个例子:
假设一组数据(20长度)为
[63,157,189,51,101,47,141,121,157,156,194,117,98,139,67,133,181,13,28,109]
现在需要按5个分桶,进行桶排序,实现步骤如下:
- 找到数组中的最大值194和最小值13,然后根据桶数为5,计算出每个桶中的数据范围为
(194-13+1)/5=36.4 - 遍历原始数据,(以第一个数据63为例)先找到该数据对应的桶序列
Math.floor(63 - 13) / 36.4) =1,然后将该数据放入序列为1的桶中(从0开始算) - 当向同一个序列的桶中第二次插入数据时,判断桶中已存在的数字与新插入的数字的大小,按从左到右,从小打大的顺序插入。如第一个桶已经有了63,再插入51,67后,桶中的排序为(51,63,67) 一般通过链表来存放桶中数据,但js中可以使用数组来模拟
- 全部数据装桶完毕后,按序列,从小到大合并所有非空的桶(如0,1,2,3,4桶)
- 合并完之后就是已经排完序的数据
时间复杂度为:O(N)+O(M(N/M)log(N/M))=O(N*(log(N/M)+1))
动态规划
https://mp.weixin.qq.com/s/3h9iqU4rdH3EIy5m6AzXsg
动态规划算法是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的方式去解决,是暴力递归的优化版本。所以做算题遇到不能直接写出的动态规划时,从暴力递归入手是个正确的选择
动态规划中包含三个重要的概念:[最优子结构],[边界],[状态转移方程]
动态规划的题目分为两大类
- 一种是求最优解类,典型问题是背包问题
- 另一种就是计数类,比如这里的统计方案数的问题,它们都存在一定的递推性质
前者的递推性质还有一个名字,叫做 「最优子结构」 ——即当前问题的最优解取决于子问题的最优解,后者类似,当前问题的方案数取决于子问题的方案数。所以在遇到求方案数的问题时,我们可以往动态规划的方向考虑。
通常如果我们察觉到了这两点要素,这个问题八成可以用动态规划来解决
暴力递归如何转动态规划
暴力递归解法->带记忆数组的递归解法->动态规划解法
自底向上和自顶向下
自顶向下
比如求f(5),递归的做法是先递归到f(1),然后再往上走得到f(5)
举个例子:
int Fibonacci(int n)
{
if(n == 0)
return 0;
if(n == 1)
return 1;
return Fibonacci(n-1) + Fibonacci(n-2);
}
为计算Fibonacci的第n个元素,我们先自顶向下地计算子问题:第n-1个元素和第n-2个元素。由于没有存储子问题的运算结果,我们给出的方法是递归。
这种方式不好,递归中会有很多重复的计算逻辑
自底向上
int array[n] = {0};
array[1] = 1;
for (int i = 2; i < n; i++)
array[i] = array[i-1] + array[i-2]
为了说明方法,采用数组存储结果,空间复杂度O(n)。事实上,额外空间可以进一步缩小到O(1):利用几个变量记录之前的状态即可。
由于我们记录了子问题的解,故给出的方法就是DP。事实上,自底向上的方式往往都是通过动态编程实现。
滚动数组思想
https://leetcode-cn.com/problems/unique-paths-ii/solution/bu-tong-lu-jing-ii-by-leetcode-solution-2/
分治法与减治法
分治法(Divide&Conquer),把一个大的问题,转化为若干个子问题(Divide),每个子问题“都”解决,大的问题便随之解决(Conquer)。这里的关键词是“都”。从伪代码里可以看到,快速排序递归时,先通过partition把数组分隔为两个部分,两个部分“都”要再次递归。
快速排序 就是典型的分治算法
减治法(Reduce&Conquer),把一个大的问题,转化为若干个子问题(Reduce),这些子问题中“只”解决一个,大的问题便随之解决(Conquer)。这里的关键词是“只”。
二分查找 就是典型的减治法
通过分治法与减治法的描述,可以发现,分治法的复杂度一般来说是大于减治法的:
快速排序:O(n*lg(n))
二分查找:O(lg(n))
贪心算法
https://www.jianshu.com/p/ab89df9759c8
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性(即某个状态以后的过程不会影响以前的状态,只与当前状态有关。)
所以,对所采用的贪心策略一定要仔细分析其是否满足无后效性。
基本思路
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题
- 对每个子问题求解,得到子问题的局部最优解
- 把子问题的解局部最优解合成原来问题的一个解
树
二叉搜索树
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(Ordered Binary Tree)或排序二叉树(Sorted Binary Tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不为空,则左子树上所有节点的值均小于它的根节点的值
- 若任意节点的右子树不为空,则右子树上所有节点的值均大于它的根节点的值
- 任意节点的左、右子树也分别为二叉查找树
- 没有键值相等的节点
完全二叉树
https://www.cnblogs.com/-citywall123/p/11788764.html
若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
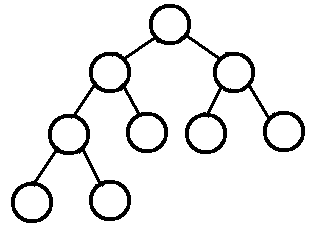
平衡二叉树
平衡二叉树的提出就是为了保证树不至于出现二叉查找树的极端一条腿长现象,尽量保证两条腿平衡。因此它的定义如下:
定义:平衡二叉树要么是一棵空树,要么保证左右子树的高度之差不大于 1,并且子树也必须是一棵平衡二叉树。
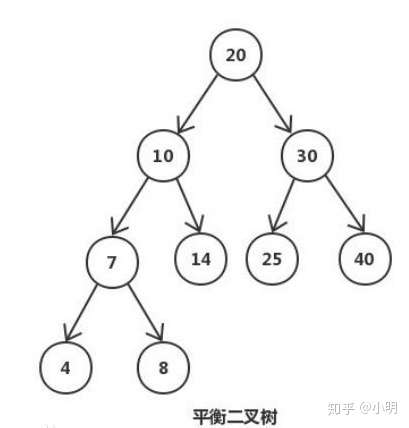
平衡二叉树是二叉搜索树
红黑树
二叉查找树并非平衡树,它只限制了左右子树与根点之间的大小关系,只有在平衡二叉查找树时,其时间复杂度才能达到O(logn) ,并且在极端情况下它甚至会退化成链表;
AVL 树是严格的平衡二叉树,必须满足所有节点的左右子树高度差不超过 1;而红黑树是相对黑色节点平衡的二叉树,
红黑树的性质
- 每个节点或者是黑色或者是红色
- 根节点是黑色
- 每个叶子节点(null)是黑色
- 如果一个节点是红色,则它的子节点必须是黑色,即两个红色节点不能直接相连
- 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑色节点
红黑树的五个性质避免了二叉查找树退化成单链表的情况,并且性质 4 和性质 5 确保了任意节点到其每个叶子节点路径中最长路径不会超过最短路径的 2 倍,即一颗树是黑红节点相间的树,另一颗全是黑节点的树;也就是红黑树是相对黑色节点的平衡二叉树;
红黑树自平衡的实现
红黑树节点的插入和删除可能会破坏上述红黑树的性质并打破它的平衡,因此需要进行调整从而让红黑树重新恢复平衡;调整分两种方式:旋转以及变色。
左旋:以 P 为旋转支点,旋转支点 P 的右子节点 R 变为父节点,其右子节点 R 的左子节点 RL 变为旋转支点 P 的右子节点;左旋之后左子树的节点相对旋转之前要多出一个节点,也就是左子树从右子树借用一个节点;
/**
* 左旋示例代码:
* P R
* / \ / \
* L R ====> P RR
* / \ / \
* RL RR L RL
* @param node 旋转支点
*/
rotateLeft(node) {
// R
const rchild = node.right;
// P.right = RL
node.right = rchild.left;
// RL.parent = P;
if (rchild.left) {
rchild.left.parent = node;
}
// R.parent = P.paretn
rchild.parent = node.parent;
// 根节点情况,
if (!node.parent) {
this.root = rchild;
} else {
if (node === node.parent.right) {
// node 是父节点的右节点,
node.parent.right = rchild;
} else {
// node 是父节点的左节点,
node.parent.left = rchild;
}
}
// R.left = P
rchild.left = node;
// P.parent = R;
node.parent = rchild;
}
右旋:如下图所示以 R 为旋转支点,旋转支点 R 的左子节点 P 变为父节点,而左子节点 P 的右子节点 RL 变为旋转支点 R 的左子节点;右旋之后右子树的节点相对旋转之前要多出一个节点,也就是右子树从左子树借用一个节点;
/**
* 右旋示例代码:
* R P
* / \ / \
* P RR ====> L R
* / \ / \
* L RL RL RR
* @param node 旋转支点
*/
rotateRight(node) {
// P
const lchild = node.left;
// R.left = RL ;
node.left = lchild.right;
// RL.parent = R
if (lchild.right) {
lchild.right.parent = node;
}
// P.parent = R.parent;
lchild.parent = node.parent;
// 根节点情况,
if (!lchild.parent) {
this.root = lchild;
} else {
if (node === node.parent.right) {
// node 是父节点的右节点,
node.parent.right = lchild;
} else if (node === node.parent.left) {
// node 是父节点的左节点,
node.parent.left = lchild;
}
}
// P.right = R;
lchild.right = node;
// R.parent = P;
node.parent = lchild;
}
变色就是由黑色节点变成红色节点或者红色节点变成黑色节点;
图论
https://zhuanlan.zhihu.com/p/25498681
图的表示
图在程序中的表示一般有两种方式:
- 邻接矩阵:
- 在 n 个顶点的图需要有一个 n × n 大小的矩阵
- 在一个无权图中,矩阵坐标中每个位置值为 1 代表两个点是相连的,0 表示两点是不相连的
- 在一个有权图中,矩阵坐标中每个位置值代表该两点之间的权重,0表示该两点不相连
- 在无向图中,邻接矩阵关于对角线相等
- 邻接链表:
- 对于每个点,存储着一个链表,用来指向所有与该点直接相连的点
- 对于有权图来说,链表中元素值对应着权重
图的遍历
深度优先遍历:(Depth First Search, DFS)
DFS通常采用 栈 数据结构
基本思路:深度优先遍历图的方法是,从图中某顶点 v 出发
- 访问顶点 v
- 从 v 的未被访问的邻接点中选取一个顶点 w,从 w 出发进行深度优先遍历
- 重复上述两步,直至图中所有和v有路径相通的顶点都被访问到
伪码实现:
//伪码实现,类似于树的先序遍历
public void DFS(Vertex v){
visited[v] = true;
for(v 的每个邻接点 W){
if(!visited[W]){
DFS(W);
}
}
}
广度优先搜索:(Breadth First Search, BFS)
BFS通常采用 队列 数据结构域
广度优先搜索,可以被形象地描述为 “浅尝辄止”,它也需要一个队列以保持遍历过的顶点顺序,以便按出队的顺序再去访问这些顶点的邻接顶点。
- 顶点 v 入队列
- 当队列非空时则继续执行,否则算法结束
- 出队列取得队头顶点 v;访问顶点 v 并标记顶点 v 已被访问
- 查找顶点 v 的第一个邻接顶点 col
- 若 v 的邻接顶点 col 未被访问过的,则 col 继续
- 查找顶点 v 的另一个新的邻接顶点 col,转到步骤 5 入队列,直到顶点 v 的所有未被访问过的邻接点处理完。转到步骤 2
要理解深度优先和广度优先搜索,首先要理解搜索步,一个完整的搜索步包括两个处理
- 获得当前位置上,有几条路可供选择
- 根据选择策略,选择其中一条路,并走到下个位置
深度优先就是,从初始点出发,不断向前走,如果碰到死路了,就往回走一步,尝试另一条路,直到发现了目标位置。这种不撞南墙不回头的方法,即使成功也不一定找到一条好路,但好处是需要记住的位置比较少。
广度优先就是,从初始点出发,把所有可能的路径都走一遍,如果里面没有目标位置,则尝试把所有两步能够到的位置都走一遍,看有没有目标位置;如果还不行,则尝试所有三步可以到的位置。这种方法,一定可以找到一条最短路径,但需要记忆的内容实在很多,要量力而行。
感悟
何时使用二分搜索
当我刷题刷多了,有一些感悟油然而生
题目中出现,给定一个按照升序排列的整数数组 (一个有顺序的数组)
这道题的解法:二分搜索
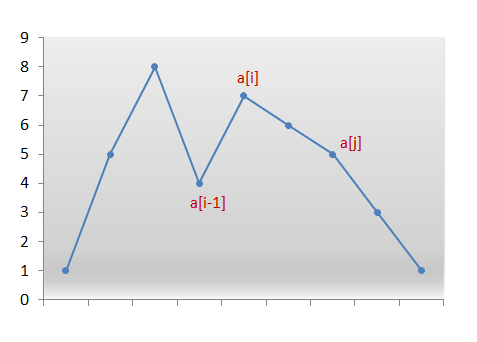
题目中出现,字典序数组,重新排序, 必须原地修改,只允许使用额外常数空间
这道题的解法:先画出数组趋势折线图
不要在if中判断0
注意数组的下标可以是0
注意数组的下标可以是0
注意数组的下标可以是0
function findScope(index, nums, target){
// 本意是index不存在才会返回
// 但是忽略了index为0的情况
if (!index) {
return [-1, -1]
}
// ...
}
正确:
function findScope(index, nums, target){
if (index == null) {
return [-1, -1]
}
// ...
}
更好的的方法
function findScope(index, nums, target){
if (index<0) {
return [-1, -1]
}
// ...
}
// 我们定义默认的index为-1
let index = -1
let nums = [1,2,3,4,5]
let target = 8
findScope(index,nums,target)
注意数组排序sort
这一点非常重要,经常会忽视的点
let arr = [2,6,4,8,10,9,15]
arr.sort()
// arr 变为 [10, 15, 2, 4, 6, 8, 9]
sort按照位数顺序进行排列,所以会出现10>2
当要判断首尾的时候
有的时候我们需要判断数组首尾是否相等,或者首尾元素是否满足一定的条件,这种情况情况下,我们通常可以考虑递归法或者栈实现。
快慢指针的判断
错误例子:
// head 是一个链表的头节点
function getEndOfHalf(head) {
let fast = head
let slow = head
// 这里不用判断slow.next
// 应该判断fast.next
if (fast.next.next && slow.next) {
fast = fast.next.next
slow = slow.next
}
return slow
}
正确的做法
// head 是一个链表的头节点
function getEndOfHalf(head) {
let fast = head
let slow = head
if (fast.next && fast.next.next) {
fast = fast.next.next
slow = slow.next
}
return slow
}
算法可接受的时间复杂度
如果你的数据规模能够达到10的5次方 ,那么很明显O(n^2)的算法就不太适合了
下面给出一个大概的数据规模和算法可接受的时间复杂度的对应表
| 数据规模 | 算法时间复杂度 |
|---|---|
| <= 10 | O(n!) |
| <= 25 | O(2^n) |
| <=100 | O(n^4) |
| <= 500 | O(n^3) |
| <= 2500 | O(n^2) |
| <= 10^6 | O(nlogn) |
| <= 10^7 | O(n) |
| <= 10^14 | O(sqrt(n)) |
| - | O(logn) |
补充
JavaScript 中数组可以保存不同类型值
https://github.com/sisterAn/JavaScript-Algorithms/issues/2
看一下 Chrome v8 源码:
// The JSArray describes JavaScript Arrays
// Such an array can be in one of two modes:
// - fast, backing storage is a FixedArray and length <= elements.length();
// Please note: push and pop can be used to grow and shrink the array.
// - slow, backing storage is a HashTable with numbers as keys.
class JSArray: public JSObject {
public:
// [length]: The length property.
DECL_ACCESSORS(length, Object)
// ...
// Number of element slots to pre-allocate for an empty array.
static const int kPreallocatedArrayElements = 4;
};
我们可以看到 JSArray 是继承自 JSObject 的,所以在 JavaScript 中,数组可以是一个特殊的对象,内部也是以 key-value 形式存储数据,所以 JavaScript 中的数组可以存放不同类型的值。
JSArray 继承于 JSObject ,从注释上看,它有两种存储方式:
- fast:存储结构是
FixedArray,并且数组长度<= elements.length(),push或pop时可能会伴随着动态扩容或减容 - slow:存储结构是
HashTable(哈希表),并且数组下标作为key
fast 模式下数组在源码里面叫 FastElements ,而 slow 模式下的叫做 SlowElements 。
快数组(FastElements)
FixedArray 是 V8 实现的一个类似于数组的类,它表示一段连续的内存,可以使用索引直接定位。新创建的空数组默认就是快数组。当数组满(数组的长度达到数组在内存中申请的内存容量最大值)的时候,继续 push 时, JSArray 会进行动态的扩容,以存储更多的元素。
慢数组(SlowElements)
慢数组以哈希表的形式存储在内存空间里,它不需要开辟连续的存储空间,但需要额外维护一个哈希表,与快数组相比,性能相对较差。
// src/objects/dictionary.h
class EXPORT_TEMPLATE_DECLARE(V8_EXPORT_PRIVATE) Dictionary
: public HashTable<Derived, Shape> {
using DerivedHashTable = HashTable<Derived, Shape>;
public:
using Key = typename Shape::Key;
// Returns the value at entry.
inline Object ValueAt(InternalIndex entry);
inline Object ValueAt(const Isolate* isolate, InternalIndex entry);
// ...
};
从源码中可以看出,它的内部就是一个 HashTable。
fast 转变为 slow
Chrome V8 源码上看,
// src/objects/js-objects.h
static const uint32_t kMaxGap = 1024;
// src/objects/dictionary.h
// JSObjects prefer dictionary elements if the dictionary saves this much
// memory compared to a fast elements backing store.
static const uint32_t kPreferFastElementsSizeFactor = 3;
// src/objects/js-objects-inl.h
// If the fast-case backing storage takes up much more memory than a dictionary
// backing storage would, the object should have slow elements.
// static
static inline bool ShouldConvertToSlowElements(uint32_t used_elements,
uint32_t new_capacity) {
uint32_t size_threshold = NumberDictionary::kPreferFastElementsSizeFactor *
NumberDictionary::ComputeCapacity(used_elements) *
NumberDictionary::kEntrySize;
// 快数组新容量是扩容后的容量3倍之多时,也会被转成慢数组
return size_threshold <= new_capacity;
}
static inline bool ShouldConvertToSlowElements(JSObject object,
uint32_t capacity,
uint32_t index,
uint32_t* new_capacity) {
STATIC_ASSERT(JSObject::kMaxUncheckedOldFastElementsLength <=
JSObject::kMaxUncheckedFastElementsLength);
if (index < capacity) {
*new_capacity = capacity;
return false;
}
// 当加入的索引值(例如例3中的2000)比当前容量capacity 大于等于 1024时,
// 返回true,转为慢数组
if (index - capacity >= JSObject::kMaxGap) return true;
*new_capacity = JSObject::NewElementsCapacity(index + 1);
DCHECK_LT(index, *new_capacity);
// TODO(ulan): Check if it works with young large objects.
if (*new_capacity <= JSObject::kMaxUncheckedOldFastElementsLength ||
(*new_capacity <= JSObject::kMaxUncheckedFastElementsLength &&
ObjectInYoungGeneration(object))) {
return false;
}
return ShouldConvertToSlowElements(object.GetFastElementsUsage(),
*new_capacity);
}
所以,当处于以下情况时,快数组会被转变为慢数组:
- 当加入的索引值 index 比当前容量 capacity 差值大于等于 1024 时(index - capacity >= 1024)
- 快数组新容量是扩容后的容量 3 倍之多时
例如:向快数组里增加一个大索引同类型值
var arr = [1, 2, 3]
arr[2000] = 10;
当往 arr 增加一个 2000 的索引时,arr 被转成慢数组。节省了大量的内存空间(从索引为 2 到索引为 2000)。
slow 转变为 fast
我们已经知道在什么时候会出现由快变慢,那由慢变快就很简单了
static bool ShouldConvertToFastElements(JSObject object,
NumberDictionary dictionary,
uint32_t index,
uint32_t* new_capacity) {
// If properties with non-standard attributes or accessors were added, we
// cannot go back to fast elements.
if (dictionary.requires_slow_elements()) return false;
// Adding a property with this index will require slow elements.
if (index >= static_cast<uint32_t>(Smi::kMaxValue)) return false;
if (object.IsJSArray()) {
Object length = JSArray::cast(object).length();
if (!length.IsSmi()) return false;
*new_capacity = static_cast<uint32_t>(Smi::ToInt(length));
} else if (object.IsJSArgumentsObject()) {
return false;
} else {
*new_capacity = dictionary.max_number_key() + 1;
}
*new_capacity = Max(index + 1, *new_capacity);
uint32_t dictionary_size = static_cast<uint32_t>(dictionary.Capacity()) *
NumberDictionary::kEntrySize;
// Turn fast if the dictionary only saves 50% space.
return 2 * dictionary_size >= *new_capacity;
}
当慢数组的元素可存放在快数组中且长度在 smi 之间且仅节省了50%的空间,则会转变为快数组
数组的动态扩容与减容(FastElements)
默认空数组初始化大小为 4 :
// Number of element slots to pre-allocate for an empty array.
static const int kPreallocatedArrayElements = 4;
在 JavaScript 中,当数组执行 push 操作时,一旦发现数组内存不足,将进行扩容。
在 Chrome 源码中, push 的操作是用汇编实现的,在 c++ 里嵌入的汇编,以提高执行效率,并且在汇编的基础上用 c++ 封装了一层,在编译执行的时候,会将这些 c++ 代码转成汇编代码。
扩容可以分为以下几步:
push操作时,发现数组内存不足- 申请 new_capacity = old_capacity /2 + old_capacity + 16 那么长度的内存空间
- 将数组拷贝到新内存中
- 把新元素放在当前 length 位置
- 数组的 length + 1
- 返回 length
整个过程,用户是无感知的,不像 C,需用用户手动申请内存空间。
当数组执行 pop 操作时,会判断 pop 后数组的容量,是否需要进行减容。
不同于数组的 push 使用汇编实现的, pop 使用 c++ 实现的。
减容可以分为以下几步:
pop操作时,获取数组length- 获取
length - 1上的元素(要删除的元素) - 数组
length - 1 - 判断数组的总容量是否大于等于 length - 1 的 2 倍
- 是的话,使用
RightTrimFixedArray函数,计算出需要释放的空间大小,并做好标记,等待GC回收 - 不是的话,用
holes对象填充 - 返回要删除的元素
稍微总结:
JavaScript 中, JSArray 继承自 JSObject ,或者说它就是一个特殊的对象,内部是以 key-value 形式存储数据,所以 JavaScript 中的数组可以存放不同类型的值。它有两种存储方式,快数组与慢数组,初始化空数组时,使用快数组,快数组使用连续的内存空间,当数组长度达到最大时,JSArray 会进行动态的扩容,以存储更多的元素,相对慢数组,性能要好得多。当数组中 hole 太多时,会转变成慢数组,即以哈希表的方式( key-value 的形式)存储数据,以节省内存空间。